From Futility Closet, a fun blog of random tidbits I enjoy reading, comes the following curious sequence of equations, attributed to J.A.H. Hunter:
I managed to extend this pattern for a few more digits before I got bored. Does it continue forever or does it eventually stop? Is there any deeper mathematical explanation lurking behind this supposed “curiosity”? What’s so special about 
The Math Less Traveled 
Taking f(x)=x^2-6 I find 264453123^2-6 = 69935454 264453123 and so on for truncations of this number, but there doesn’t appear to be such a pattern for f(x)=x^2-1
It starts here: http://oeis.org/A151752 Hint: look at the leading digits.
Fascinating! However, the pattern seems not to continue: the 13th term in that sequence is 3773193359375, suggesting that
ought to end in 377319335937, but it is actually equal to 284739762543877319335937 instead! In fact, the right digit to use here is 8: 
.
What’s the connection to all-odd-digit number divisible by powers of 5, and why does the pattern stop?
One (obvious) thing I see here is that the pattern basically says that a number of the form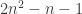
is divisible by a large power of 10. Maybe I’ll have time to look at more details tonight.
It seems to stop at 88384389877319335937
Actually, my code had a bug that did not account for the first zero in the sequence! It certainly seems to go on forever:
…5548722601433298591064947197786574820441719412220106407559357953405720
0770206342858319449522214639585592951097866225470440776483509324976437
1295716500836135134846344163506159929966088384389877319335937
Cool, what language did you use to implement that? Can you share your code?
I used Mathematica. Here is the code I used:
digs = {7};
Module[{d},
Do[
d = Select[Range[0, 9],
Module[{t},
t = digs~Prepend~#;
FromDigits[t] ==
Mod[2 FromDigits[t]^2 – 1, 10^(Length[digs] + 1)]] &][[1]];
digs = digs~Prepend~d
,
{200}
];
];
FromDigits[digs]
It assumes that there is always some digit that will work, and selects the first one that works in each iteration. It seems to work so far.
Your assumption is valid. There is always exactly one number that works to continue the sequence. What’s more, that number depends completely on the digit of 2n^2-1 appearing immediately before n appears. I haven’t found a better way to find that digit yet other than simply computing 2n^2-1 out to enough digits though.
It seems like there should something to say concerning 10-adic numbers, but I’m not sure what.
I thought of that too, but didn’t follow it up because I thought the p-adic numbers are only defined when p is prime. But after your comment I dug a little deeper and realized that although the n-adic numbers for n composite do not form a *field* they do still form a *ring*, which is just fine for the purposes of this problem.
I conjecture the following: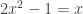
, considered as an equation in the ring of 10-adic numbers, has a unique solution, of which 7, 37, 937, … are all suffixes.
Hmm, this is not quite right (re: unique solution), since the 10-adics admit the solutions 1 and (-1/2) = …99999.5, just like the reals. But it seems the 10-adics also admit one other, weirder solution…?
An interesting link sent to me by Matt Gardner Spencer, which seems relevant: http://www.numericana.com/answer/p-adic.htm#decimal
I wonder if it is possible to come up with an algorithm for generating the infinite sequence without using brute-force guessing. One simple observation: any such algorithm will necessarily use an unbounded amount of memory; a bounded-memory algorithm would produce a periodic sequence, but periodic 10-adic numbers are equivalent to negative rationals, and we know there are no rational solutions other than 1 and -1/2.
Let k_i denote the number just to the left of the gap (running down the pyramid) in the i-th row. Then d_{i+1} (the next digit to be prepended) is 7k_i mod 10. So getting the next digit from the previous line is straightforward. But finding k_{i+1} seems to require both k_i and the digit to the left of k_i, at least the way I’m approaching it. That means it’s really no better than simply computing k_{i+1} with brute force ((2x^2-x-1)/10^{i+1} mod 10)
Hmm, well, but at least that gives a way of directly computing each successive digit (rather than having to guess and check).
Using this method I have computed the first 20,000 digits (takes about 15 seconds on my computer). You can find them here.
Pingback: An invitation to a funny number system | The Math Less Traveled
Pingback: The decadic metric | The Math Less Traveled
Pingback: More fun with infinite decadic numbers | The Math Less Traveled