In a previous post, I challenged you to prove
If
evenly divides
, then
evenly divides
,
where denotes the
th Fibonacci number (
).
Here’s one fairly elementary proof (though it certainly has a few twists!). Pick some arbitrary and consider listing not just the Fibonacci numbers themselves, but their remainders when divided by
. For example, let’s choose
, so we want to list the remainders of the Fibonacci numbers when divided by
.
Here are the first 17 Fibonacci numbers:
And here are their remainders when divided by , represented graphically (red = 1, orange = 2, blank gap = 0):
And indeed, as we would expect if the theorem is true, every fourth remainder is zero: is evenly divisible by
. But there seems to be a bit more than that going on—the pattern of remainders we got is definitely not random! Let’s try
. Here are the remainders when the first 21 Fibonacci numbers are divided by 5:
Hmm. Every fifth remainder is zero, as we expected… but the other remainders don’t seem to follow a nice pattern this time.
…or do they? Actually, if you stare at it long enough you’ll probably find some patterns there! Not to mention that I haven’t really shown you enough of the sequence. Here are the remainders of the first 41 Fibonacci numbers when divided by 5:
Aha! So it does repeat after all. We just hadn’t looked far enough.
And just for fun, let’s include some Fibonacci numbers mod . These repeat much more quickly than for
.
OK, now that we’ve tried some specific values of , let’s think about this more generally. When listing the remainders of the Fibonacci numbers divided by
, the initial part of the list will look like
because all the Fibonacci numbers before are of course less than
, so when we divide them by
they are simply their own remainder. Next, of course,
leaves a remainder of zero when divided by itself. Then what?
Well, by definition, so its remainder mod
is
. OK, so far we have
In fact, the rule for finding the next remainder in the sequence will be the same as the rule defining the Fibonacci numbers, except that we do everything mod . So the next element in the sequence is
again:
…and now, it seems, we are stuck! What do we get when we add ? Who knows?
Here is where I will do something sneaky. I am going to replace the second copy of by
, like this:
Huh!? What does that even mean? Surely we can never actually get a negative number as a remainder when dividing by . Well, that’s true, but from now on, instead of strictly writing the remainder when
is divided by
, I’ll just write something which is equivalent to
modulo
. This is all that really matters, since I just want to see which positions are equivalent to zero modulo
.
So, the claim is that . Why is that? Well,
, and then we can just subtract
from both sides.
Then what? ; then
, and so on: we get the Fibonacci numbers in reverse, with alternating signs!
For example, here are the first few Fibonacci numbers mod 8 again, but according to the above pattern, with negative numbers indicated by downwards pointing bars (and the original bars shown mostly transparent, for comparison):
See how the colors of the bars repeat now, but running forwards then backwards?
If is even, then
will be positive (as you can see in the example above); that is, we get
After this point we get , and so on, and the whole pattern repeats again, as we’ve seen.
What if is odd? Then
will be negative, so we have to go through one more cycle with everything negated:
This explains why we had to look at a longer portion of the remainders mod 5 before they repeated. Here’s mod 5 again, with negatives shown graphically:
The colors of the bars still repeat: forwards, then backwards but alternating up and down, then forwards but all upside down, then backwards and alternating (but the other way). But at the end we’re back to , so the whole thing will repeat again.
In any case, whether is odd or even, these patterns of remainders will keep repeating forever, with a
always occurring every
positions—that is, at
, so
will always be divisible by
!
There are other ways to prove this as well; perhaps I’ll explain some of them in a future post. It turns out that the converse is also true: if evenly divides
, then
must evenly divide
. I don’t know a proof off the top of my head, but maybe you can find one?







Great explanation! I especially like the diagrams illustrating sign changes.
I think your proof here also shows the converse: If does not divide
does not divide  , then the remainder of
, then the remainder of  modulo
modulo 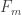 is one of
is one of 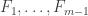 (possibly negated) and is therefore nonzero.
(possibly negated) and is therefore nonzero.
Oh, hey, what do you know! I proved something without realizing it. What should we call this proof technique? “Proof by golly”?
Pingback: Mathblogging.org Weekly Picks « Mathblogging.org — the Blog
Pingback: Fibonacci numbers in Art « Wed-Gie
Pingback: Fibonnaci Frency « ElephantsWind