This post is a special shout-out to my former students who are now taking calculus (if you don’t know any calculus, just hang tight… there will be more calculus-less math goodness coming your way soon). This post is 100% money-back guaranteed to not really help you at all on the AP exam! But don’t worry, it’s still awesome.
First, consider this equation:
Perhaps you’ve seen it before… among other things, it gives us a very neat connection between complex numbers expressed in polar coordinates (
Let’s set 
So we write this observation as a simple differential equation; after swapping 
And since 
Now for a really good time, set 
Almost makes you cry, doesn’t it? It relates five of the Most Important Numbers in the World (0, 1, e, i, and 
And for a short time only, this equation can be yours for the low, low price of the number of grains of rice on the last square of a chessboard if you put just one grain on the first square, two grains on the second square, four grains on the third, and merely double the number of grains each time. Order now, supplies are limited!
The Math Less Traveled 
Pingback: Carnival of Mathematics IX « JD2718
Hi Brent — I enjoyed reading this! I always wished I could make friends with complex variables, and your post made me feel like it might be possible. 🙂
Hi Alane, glad you enjoyed it! There’s nothing really that complex (haha) about complex variables, as long as you understand complex numbers and just follow things through to their logical conclusions.
great brent! truly great. i knew of this equation and loved it but i had never thought of proving it the way you did it. i always went by the maclaurin’s series method. i enjoyed reading this.
cheers!
vinit
I knew it was the most beautiful eqn.. now i found y it is so… thnks
Cool!!!, and I can even understand it!!
Awesome page dedicated to a most fantastic and worth-while result!!!
I teach Calculus I & II at a public school in Upstate New York and I can assure you, as soon as my students make it to a point where they will be able to fully follow each of the steps, they will be directed to this site. Once they digest and understand the proof so that they can re-create the end result and demonstrate it to me personally, they will be richly rewarded!!!
Thank you!
Hi Murray,
Excellent! I hope your students enjoy it. You may also be interested to know that I am planning at some point in the near future to write about a really neat paper by Ivan Niven proving the irrationality of pi, using only elementary calculus — your students might enjoy that as well.
Hi Brent,
I look forward to seeing your next posting regarding pi. When it’s set, I hope you leave a link to it on this page.
Hi Murray,
It doesn’t particularly make sense to put a link to future posts on this page, but I would be happy to send you an email when I start that series of posts. Alternatively, you could subscribe to the blog (using either an RSS reader such as Google Reader, or via email by filling out the subscription form in the sidebar) and be automatically notified when I make new posts.
Pingback: Trig sum identities, the easy way « The Math Less Traveled
Pingback: 8 Jan « Maineiac
Great! I’ve got my (2^64)-1 grains of rice ready!
Even though it was kinda mentioned already, I wanted to add that I would not have passed my calc AP exam if I had not known this… I used it to derive all my trig identities so I didn’t have to memorize them.
I want my 100% money back now…
Hi
Nice post… But have a doubt…
When you say:
ln(z) = i*theta + C
for theta=0
z = cos(0) + i*sin(0) = 1
putting this in the above
ln(1) = 0 + C
=> C = 0 (as log of 1 for any base is 0)
Also even if C = 1
z=e^(i*theta + C)
So, how come you got C=1
If I am wrong please correct …..
Anyway…. Thanks for the nice post
favonius: Aha, very perceptive! You are absolutely right that if we solve ln z = i*theta + C for C, we get C = 0. So what happened? The answer is that I sort of cheated! =)
Think about how we get from ln z = i*theta + C to the next line, z = Ce^(i*theta). We got there by taking e raised to the power of both sides, so
e^(ln z) = e^(i*theta + C)
z = e^(i*theta) * e^C
So why did I write ‘C’ instead of ‘e^C’ on the second line? Well, the point is that if C is a constant, then e^C is also a constant — so I just wrote ‘C’ to mean ‘some constant’. But I cheated a bit because it is not the *same* constant as the one in the previous equation! This is actually fairly standard, but it can certainly be confusing if you’ve never seen it before. It would have been more clear if I had written
ln z = i*theta + C_1
and then
z = C_2 * e^(i*theta)
where, of course, C_2 = e^(C_1). Now we can see that things match up: C_1 = 0, as you found, and C_2 = 1 as I argue in the post; and 1 = e^0 as expected.
Pingback: PentaMath.com » Blog Archive » Mathematical Beauty
isn’t the integral of 1/x = lnx + C? How do we get rid of it? Gosh, so many constants to worry about.
Otherwise, love this entry.
You know, I’m cool with there being only one C in the equivalence lnx = i*theta + C. One C plus or minus some other C is just gonna be another C, anyway. Good, good, good.
However, the antilog of 1/x is ln|x|, right? So doesn’t that mean that Ce^(i*theta) = |z|? And doesn’t that screw up our wonderful equation? Because now when theta = pi, our right hand side is +1 instead of -1!
Please save me from myself 🙂
Hi Candy,
Good catch! You’re right that the antiderivative of 1/x is really ln |z|. Then we get Ce^(i*theta) = |z|, and therefore z = +/- e^(i*theta) (since C = 1). Remember that we characterized z as something for which differentiating and multiplying by i are the same–and indeed, this more careful analysis has shown that there are actually *two* expressions with this property, e^(i*theta) and -e^(i*theta). So in reality this was not quite enough to completely characterize the expression cos(theta) + i*sin(theta); to complete the analysis we would have to note that -e^(i*theta) can’t be equal to cos(theta) + i*sin(theta), since (for example) it is easy to see that they are not equal when theta=0.
Euler would be very very proud indeed!
Such confusion such headache.. why would one need to make such high brain puzzling mathmatical equations…. i understand algebra… i understand geometry… but trig or calc?
Pingback: Euler’s Identity Formula « Ishango Bones
Great post! I’ve seen Euler’s Identity many times, but never bothered to look for a good proof and try to understand it. As I’m planning to major in electrical engineering I have a feeling this new understanding will be most helpful.
Hi Brent,
I’m 65 and my math ended with diffy Q’s, is it still called that, and I’ve tried, for fun, to brush up and it’s just to difficult because I’ve forgotten so much Algebra. It’s still fun trying to figure out what your doing, I envy the younger student of Math.
Thanks FCorley
Hi Frank,
Thanks for your message! You probably mean “diff EQ’s” which is short for “differential equations”, and yes, it’s still called that. =) Glad you are having fun! Feel free to post questions when there are things you don’t understand.
Hi Brent,
Isn’t it a problem to take the logarithm of a complex number? I mean, I know the log function on part {x>0} of the real line, but how do you define log(-1/2 + sqrt(3) i/2)? Or log(-1)?
If there is a complex logarithm, is it still a function? (The equation e^(i theta)=z has many solutions…)
Tastalian: good point! It is in fact possible to define a complex logarithm as the inverse of complex exponentiation—but since complex exponentiation is not one-to-one, the inverse does not technically exist, exactly as you say. There are ways around this by carefully specifying which solutions we mean, but you’re right that to make this argument completely rigorous would require a lot more careful attention!
I vaguely remember some theorem in calculus, given two functions f and g, if the functions have the same value at zero, and all derivatives also match at zero, then the functions are identical. Using that theorem, it is not hard to prove by induction the following:
sin x = 1 – x^3/3! + x^5/5!…
cos x = x^2/2! – x^4/4!…
e^x = 1 + x^2/2! + x^3/3!…
And from these it is easy to show that e^x = cos ix – i sin ix, and if you let a=ix, then e^ia = cos a + i sin a. Now simply substitute a = pi, and you get the Most Beautiful Equation.
Errata: at the last step, just substitute x = i pi. Nevermind about a.
Do you really want 4.54 Ă— 10^13 kilograms rice?
This is around the total production for all cereal grains in the world. Nice example of Eulers thm. What are you using to set eqs? TeX?
Yes, it is a joke. =) And yes, I use LaTeX to typeset equations.
Pingback: The Most Beautiful Equation in the World « The Math Less Traveled | Evan Stein's Internet Studio
It’s been many years but can’t this beautiful equation also be proven through a Taylor Series Expansion?
Dave: yes, definitely! See John Henckel’s comment above.
why we take theta in radians??
Here I got an equation y^(ix)=-1, at least (x=pi,y=e) is its solution. Is it the unique solution for this equation?
Yanmin: no, there are infinitely many solutions: for example, (x=2pi, y = sqrt(e)) is also a solution. In general (x=k*pi, y = e^(1/k)) will be a solution for any nonzero real number k.
David: because the facts that the derivative of sin is cos and the derivative of cos is -sin are only true for the versions that take radians as arguments. Radians are an extremely natural unit of measurement for angles because they are simply defined in terms of radius and arc length.
nice prove!
i liked it very much
OMG im in yr8 an we hd a question in our hmwrk 4 dis and it basically gve me da answa dnt tel any1 doh! LOL:P
2^63 grains
i like the equation but not the headache
Does it mean that there is a universal pattern to the world?
Like the circle
I think the universe works like a circle.
When suns explode and compress under their own weight I think that they compress beyond our dimension and go into the 4th dimension of time. I think like most critical breaks there is a critical point or value at which it will break into the 4th dimension. I think such an event could produce a large event at one point in time. We know of one such event ‘the big bang’
Does this mean that the universes creation was from it’s eventual destruction.
That would be cool.
I think too much.
Sorry I have just never met smart people before I really don’t know what to say
i also like using the power series method:
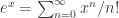
you can watch the imaginary parts alternate about the complex plane and converge to the real value -1.
Well, what you did was an over kill…. you didn’t see it. New to this?
take your first equation, set theta = pi, then your solution is right there. No sense in taking the derivative, then integrate (which takes you back before your derivative). That was pointless and extra work that was not needed.
e^i(theta) = cos(theta) + isin(theta) This is your first equation, set theta to pi,
e^i(pi) = cos(pi) + isign(pi)
e^ i(pi) = -1 + 0
e^i(pi) +1 = 0 wow, no useless calculus, same result.
Hi Jim, maybe you didn’t read the post very carefully. You’re absolutely right that the equation involving e, i, and pi comes from just setting theta to pi in that first equation
. All the calculus was to explain why that equation is true in the first place. It was only “overkill” if you’re willing to take that equation on faith!
you can do it in a simpler way.
let f(x) = (cosx + i sinx)/exp(ix). unlike the original post, it doesn’t even need to be demonstrated that the function _means_ anything sensible. you only need to accept for the sake of argument is that “i” is a number with the trait i^2 = -1
df/dx is identically zero, so it satisfies the terms of the mean value theorem for derivatives and therefore it follows (using [0,x] or [x,0]) that f(x) = f(0) = 1. nothing more advanced than part of a first semester of calculus and the definition of “i” is required, and the result is (AFAIK) rigorous.
PS i believe cauchy’s integral formula is superior still to euler’s formula, though EXPiPI fits on a license plate 🙂