Did you know that the ratio between the side of any triangle and the sine of the opposite angle is equal to the diameter of the triangle’s circumcircle? I didn’t! I just learned it today when researching the law of sines. All that time spent on the law of sines in high school, and no one ever bothered to tell me that in any triangle, not only are all the ratios between side lengths and sines of opposite angles equal to each other, they are also equal to something else interesting — namely, the diameter of the circumcircle!
Among other things, this means in particular that if you inscribe any angle in a circle with diameter one, the length of the chord it subtends is equal to the sine of the angle:
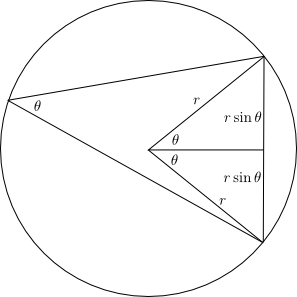
Nifty, eh? Want to see a proof? Here it is:
Rather than explain it in detail, I’ll just let you stare at it for a while, and leave a comment if you have questions. =) The one thing you need to remember from geometry that you might not remember is that an angle inscribed in a circle (like in the above picture) subtends an angle twice as large.


Pingback: Three trigonometry topics — The Endeavour
Cool stuff! I hadn’t seen that before. From here, you can find the ratio of the area of the circumscribed circle to the area of the triangle.
The triangle has area .5*AB*Sin(c)
The circle has area Pi*D^2/4, with D = C/Sin(c) = B/Sin(b) = A/Sin(a). D^2 = AB/[Sin(a)Sin(b)]. Taking all this and plugging it in together we get:
A_circ/A_tri = Pi*AB*2/[4*Sin(a)*Sin(b)*AB*Sin(c)]
= Pi/[2*Sin(a)*Sin(b)*Sin(c)]
Pingback: Elegant proofs 3 « Newton Excel Bach, not (just) an Excel Blog
I am often frustrated by textbooks that write the law of sines with the angle as the numerator, thus forcing the geometric evidence out of the problem. As I write in http://www.pballew.net/lawofsin.html
“I am frequently amazed to see this theorem presented in math texts without the “=2r” which seems to give it visual or geometric life. It is especially curious since the property dates back to Ptolemy.”
Pingback: Let’s Read the Internet! week 8 « Arcsecond
Pingback: Richard Elwes - The sine of the beast
Gorgeous. And I really didn’t know it.
I would have proved it simply by noticing that the angle opposite to the diameter of the circle is a right angle..
Muhammad: It is certainly a good check to ensure that this makes sense when theta is a right angle, but unfortunately that is not a proof that this works for any angle theta. For example, what if I said that when the angle is theta, the length of the chord is 1? This works when theta is a right angle, but obviously that does not mean it is true for any angle.
Sorry, but I need to explain myself a little more. Note that I didn’t mean that my proof is any better than yours.
Case 1: Take the special case when one of the two sides of the angle \theta is a diameter. Then the length of that diameter is 1, and the angle against the diameter is right angle so we get a right angle triangle with the length of the chord opposite to \theta equal to sin(\theta)*hypotenuse(=1) which is sin(\theta).
General Case: For the general case (as in the diagram) all the angles on the chord are equal (equivalent to all subtending an angele twice as large), so we can select one of these angles, namely one that has a diameter as a side, which gets us to case 1.
As I said, it is more or less the same as your method. It is just that that’s the way I first thought of it..
Aha, now I understand. Don’t apologize, your proof IS better than mine! =)
I didn’t know this, and I feel like I was cheated by my geometry teacher.
I feel like I should have known this — I am a math professor with a Ph.D. — but I’m comforted to hear that a lot of other people didn’t know about it, either.