The Riemann zeta function and prime numbers

In a previous post I defined the famous Riemann zeta function,

$\displaystyle \displaystyle \zeta(s) = \sum_{n \geq 1} \frac{1}{n^s}.$

Today I want to give you a glimpse of what it has to do with prime numbers—which is a big part of why it is so famous.

Consider the infinite product

$\displaystyle \left(\frac{1}{1-2^{-s}}\right)\left(\frac{1}{1-3^{-s}}\right)\left(\frac{1}{1-5^{-s}}\right)\left(\frac{1}{1-7^{-s}}\right) \dots \left(\frac{1}{1-p^{-s}}\right) \dots$

where each sequential factor has the next prime number raised to the $-s$ power. Using big-Pi notation, we can write this infinite product more concisely as

$\displaystyle \prod_{p \text{ prime}} \frac{1}{1 - p^{-s}}$

(The big $\Pi$ means a $\Pi$ roduct just like a big $\Sigma$ means a $\Sigma$ um.)

Now let’s do a bit of algebra. First, recall that the infinite geometric series $1 + r + r^2 + r^3 + \dots$ has the sum

$\displaystyle 1 + r + r^2 + r^3 + \dots = \frac{1}{1-r},$

as long as $r < 1$ . (For some hints on how to derive this formula if you haven’t seen it before, see this blog post or this one.) Of course, $1/(1-p^{-s})$ is of this form, with $r = p^{-s}$ . Note that $p^{-s} = 1/p^s$ which is less than $1$ as long as $s > 0$ , so the geometric series formula applies, and we have

$\displaystyle \prod_p \frac{1}{1 - p^{-s}} = \prod_p (1 + p^{-s} + p^{-2s} + p^{-3s} + \dots)$

(From now on I’ll just write $\prod_p$ instead of $\prod_{p\text{ prime}}$ .) That is,

$\displaystyle (1 + 2^{-s} + 2^{-2s} + \dots)(1 + 3^{-s} + 3^{-2s} + \dots)(1 + 5^{-s} + 5^{-2s} + \dots) \dots$

So this is an infinite product of infinite sums! But you’re not scared of a little infinity, are you? Good, I thought not. Now, what would happen if we “multiplied out” this infinite product of infinite sums? Note that every term in the result would come from picking one term of the form $p^{-ks}$ from each of the factors, one for each prime $p$ , and multiplying them. (Though infinitely many of the choices have to be $1 = p^{-0s}$ if we are to get a finite term as a result.) For example, one way to choose terms would be

$\displaystyle 1 \cdot 3^{-2s} \cdot 5^{-s} \cdot 1 \cdot 13^{-3s} \cdot 1 \cdot 1 \cdot \dots$

which would give us $(3^2 \cdot 5 \cdot 13)^{-s} = 585^{-s}$ . In fact, because of the Fundamental Theorem of Arithmetic (every positive integer has a distinct prime factorization), each choice gives us the prime factorization of a different positive integer, and conversely, every positive integer shows up exactly once. That is, after multiplying everything out, we get one term of the form $n^{-s}$ for each positive integer $n$ :

$\displaystyle \prod_p \frac{1}{1 - p^{-s}} = \sum_{n \geq 1} n^{-s} = \sum_{n \geq 1} \frac{1}{n^s}$

But that’s just our old friend $\zeta(s)$ ! So in fact,

$\displaystyle \zeta(s) = \prod_p \frac{1}{1 - p^{-s}}$

turns out to be an equivalent way to write the Riemann zeta function.

We can now use this in a really cute proof that there are infinitely many primes. Consider $\zeta(1)$ , where we substitute $1$ for $s$ . In our original definition of $\zeta$ , we get

$\displaystyle \zeta(1) = \sum_{n \geq 1} \frac{1}{n} = 1 + 1/2 + 1/3 + 1/4 + 1/5 + \dots$

This is known as the harmonic series, and it is a well-known fact that it diverges, that is, as you keep adding up more and more terms of the series, the sum keeps getting bigger and bigger without bound. Put another way, pick any number you like—a hundred, a million, a trillion—and eventually, if you keep adding long enough, the sum $1 + 1/2 + 1/3 + 1/4 + 1/5 + \dots$ will become bigger than your chosen number. (Though you may have to wait a very long time—the harmonic series diverges rather slowly indeed!) One way to prove this is to note that the series $1 + 1/2 + 1/3 + 1/4 + 1/5 + \dots$ is greater than

$\displaystyle 1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + (1/16 + \dots) + \dots$

(the original series is greater than this because we only made some of its terms smaller—I changed the $1/3$ into $1/4$ , and then changed $1/5$ through $1/7$ into $1/8$ , and then $1/9$ through $1/15$ into $1/16$ , and so on). But this new smaller series is equal to $1 + 1/2 + 1/2 + 1/2 + 1/2 + \dots$ which will clearly get arbitrarily large. So the harmonic series, which is larger, must diverge as well.

So, $\zeta(1)$ diverges. But what happens if we plug $s = 1$ into the other expression for $\zeta(s)$ ? We get

$\displaystyle \prod_p \frac{1}{1 - p^{-1}} = \prod_p \frac{1}{1 - 1/p} = \prod_p \frac{p}{p-1}.$

If there were only finitely many primes, this would be a finite product of some fractions and would thus have some definite, finite value—but we know it has to diverge! Thus there must be infinitely many primes.

I will note one other thing—when I was writing up some notes for this post I was initially confused by the fact that if we set, say, $s = 2$ , we already know that $\zeta(2) = \pi^2/6$ ; but now we also know that

$\displaystyle \zeta(2) = \prod_p \frac{p^2}{p^2 - 1} = \frac{4}{3} \cdot \frac{9}{8} \cdot \frac{25}{24} \cdot \frac{49}{48} \cdot \frac{121}{120} \dots$

But this is an infinite product of fractions which are all bigger than $1$ ! How could it converge? …well, my intuition was just playing tricks with me. Although I have lots of practice thinking about infinite sums that converge, I am just not used to thinking about infinite products that converge. But in the end it is not really any more surprising than the fact that an infinite sum can converge even though all its terms are positive: as long as the fractions are getting smaller quickly enough, such an infinite product certainly can converge, and in fact it does. Using a computer confirms that the more terms of this product we include, the closer the product gets to $\pi^2 / 6 \approx 1.64493\dots$

About Brent

Associate Professor of Computer Science at Hendrix College. Functional programmer, mathematician, teacher, pianist, follower of Jesus.

View all posts by Brent →

15 Responses to The Riemann zeta function and prime numbers

Anon says:

March 6, 2017 at 9:00 pm

From the last computation you can also note that the fact that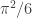 $\pi^2/6$ is irrational implies that there are infinitely many primes (because a finite product of rational numbers is rational).
- Brent says:
  
  March 6, 2017 at 9:43 pm
  
  Ah, good point! Though I have to ask — how do you know that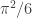 $\pi^2/6$ is irrational?
  - sn0wleopard says:
    
    March 8, 2017 at 5:17 pm
    
    Let’s assume that x = pi^2/6 is rational. Then, pi = sqrt(6x), which is merely irrational, not transcendental. So, it seems that we’ve reached a contradiction 🙂
    - sn0wleopard says:
      
      March 8, 2017 at 5:52 pm
      
      P.S.: The above actually proves a stronger result: pi^2/6 must be transcendental.
    - Brent says:
      
      March 8, 2017 at 9:05 pm
      
      Indeed, so this depends on knowing $\pi$ is transcendental — a rather big result! Using the transcendence of $\pi$ to prove the infinitude of the primes is like dropping an anvil on a mosquito. (Which can be rather fun, of course.) (Though to be sure, I don’t know whether the proof of the transcendence of $\pi$ already depends on the infinitude of primes…)
      - sn0wleopard says:
        
        March 9, 2017 at 5:41 pm
        
        Good point! 🙂 Our of curiosity I decided to check the proofs of the transcendence of pi, and the first one I found does indeed seem to depend on the infinitude of primes: https://en.wikipedia.org/wiki/Lindemann%E2%80%93Weierstrass_theorem — it requires picking a sufficiently large prime p in one of the preliminary lemmas. Crazy!
        
        Brent says:
        
        March 9, 2017 at 8:04 pm
        
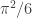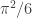        Hah! Good detective work. So this doesn’t work after all — pity! On the other hand, it’s quite possible there is a more elementary way to establish that $\pi^2/6$ is irrational, but I am not sure. I know how to prove $\pi$ is irrational, but off the top of my head I don’t see an easy way to modify the proof to work for $\pi^2/6$ . 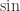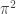(The proof depends on the fact that $\sin$ and $\cos$ vanish at $\pi$ ; so the modified proof would have to involve a function that vanishes at $\pi^2$ , but functions like $\sin(\sqrt{x})$ would make things really messy since you end up taking iterated derivatives.)
        
        sn0wleopard says:
        
        March 9, 2017 at 8:14 pm
        
        I’d be interested to see the proof if you manage to make it work!
        
        Brent says:
        
        March 9, 2017 at 8:17 pm
        
        Oh, I’m not going to spend any more time on it! But if you want to see the proof of the irrationality of pi, go to https://mathlesstraveled.com/post-series/ and scroll down to “Irrationality of Pi”. (Or you can just read the original paper by Niven here: http://projecteuclid.org/euclid.bams/1183510788 .)
        
        sn0wleopard says:
        
        March 9, 2017 at 8:31 pm
        
        Great, thanks!
Naren Sundar says:

March 6, 2017 at 9:38 pm

I haven’t thought about infinite products converging before but I was just wondering if it is possible to analyze convergence of infinite products by taking their `log` version and looking at the infinite sum instead?
- Brent says:
  
  March 6, 2017 at 9:42 pm
  
  Good question! I am not an expert in this area, but I can’t think of any reason why this wouldn’t work.
- Xander Henderson says:
  
  March 7, 2017 at 8:19 am
  
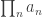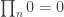  Indeed, this is generally the way that the convergence of infinite products is handled. By definition (or, at least, by the usual definition), an infinite product $\prod_n a_n$ is said to converge if and only if the corresponding sum $\sum_n \log(a_n)$ converges. Note that this implies (for example) that the infinite product $\prod_n 0 = 0$ does NOT converge. In general, in order for an infinite product to converge, it cannot “converge” to either 0 or infinity!
Curtis Bechtel says:

March 7, 2017 at 5:07 pm

I think you meant to say ‘greater than’ when you compared the harmonic series to 1 + 1/2 + (1/4 + 1/4) + …
- Brent says:
  
  March 7, 2017 at 8:52 pm
  
  Good catch, thanks! Fixed now.