And now for something completely different!1
Suppose we have a parallelogram with one corner at the origin, and two adjacent corners at coordinates and
. What is the area of the parallelogram?

There are probably many different ways to derive the answer; post your ideas in the comments!

An easy way is simply to take the magnitude of the cross product of and
and 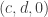 !
!
Yes – but why?
Directly from the cross product: S = |ad-bc|
The parallelogram can also be seen as the sum of two triangles with the same area, or four right triangles with the same area.
Wait, how do you cut it up into four right triangles with the same area?
huuuu. Yes, you are right, there are not right triangles with the same area for a general parallelogram. Actually, it is always possible to build up two right triangles in the semi-parallelogram, but they have different areas. This may be visualized easily taking a rectangle, that is b = c = 0 or a = d = 0 (Geogebra is helpful).
Area = (a + c – b)*d – b^2
Mark a rectangle with bottom left corner at (0,0) and top right at (a+c, b+d).
ie The top right corner of the parallelogram and rectangle match.
Obtain parallelogram area by:
Area of rectangle minus area of the triangles formed between the rectangle and parallelogram on the 4 sides.
There’s a typo in the above.
The parallelogram area should read:
Area = a*(b + d) – b*(a + c)
Two parallelograms between the same parallels that share a base have the same area.
Let’s call the parallelogram with
with 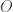 at the origin and the rest of the vertices counterclockwise. The line
at the origin and the rest of the vertices counterclockwise. The line 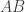 passes through the points
passes through the points  , has a slope of
, has a slope of  , and an
, and an 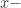 intercept of
intercept of 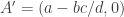 . The point
. The point  lies on the same line.
lies on the same line.
The two parallelograms are both between the parallels
are both between the parallels  , and share
, and share  as a base. Therefore they have the same area.
as a base. Therefore they have the same area.
The area of a parallelogram is equal to the product of the length of a base and the length of its altitude. For parallelogram , the length of side
, the length of side 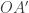 is
is  and the altitude is of length
and the altitude is of length  , giving an area of
, giving an area of 
I like the shoelace formula, which works for any polygon. To see why it works is much the same as understanding the final formula for the parallellogram though. I like to think about it as the trapezium rule, but extended from a function to a curve.
points: ,
,  .
.
shoelace formula: .
.
trapezium rule: .
.
Yes, one of the places I’d eventually like to go is deriving a proof of the shoelace formula. Understanding the formula for the (signed) area of a parallelogram is one of the first building blocks along the way!
ad – bc
I enclosed the parallelogram in a rectangle that has a length of a+c and a width of b+d. I calculated the rectangle’s area and then split the negative space outside the original parallelogram into 2 congruent trapezoids and 2 congruent triangles. Subtracting the areas of those 4 figures from the area of the rectangle yields ad – bc.
The volume interpretation of the determinant gives some nice generalisations. The determinant is the factor involved in the change of variables formula. This gives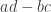 for the area, because it is the determinant of the matrix
for the area, because it is the determinant of the matrix  which maps the unit square (of area 1) to the parallelogram. And, for example, the area of the ellipse inscribed in the parallelogram is
which maps the unit square (of area 1) to the parallelogram. And, for example, the area of the ellipse inscribed in the parallelogram is  , since the circle inscribed in the unit square has area
, since the circle inscribed in the unit square has area  . The determinant also generalizes to higher dimensions.
. The determinant also generalizes to higher dimensions.
We want an operation on that gives us the area of the parallelogram they span. Let’s call it
that gives us the area of the parallelogram they span. Let’s call it  . We want to say that
. We want to say that  is linear—that is,
is linear—that is, 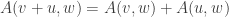 ,
, 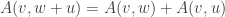 , and for any real number
, and for any real number  ,
, 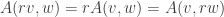 (you can see this for natural
(you can see this for natural  by tiling parallelograms). But for this to work with negative
by tiling parallelograms). But for this to work with negative  , we’ll actually have to consider *signed area*, or area with specified orientation, so that
, we’ll actually have to consider *signed area*, or area with specified orientation, so that 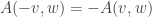 . Now we can see that we want
. Now we can see that we want 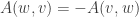 (which implies
(which implies  ), and we’ll normalise by saying the unit square has area 1:
), and we’ll normalise by saying the unit square has area 1: 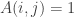 where
where 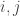 are standard unit vectors.
are standard unit vectors.
Now, we can calculate the (signed) area of the parallelogram spanned by (a,b) and (c,d):
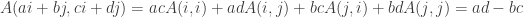 .
.
So the unsigned area is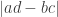 .
.
This is a neat analysis. The only part I don’t follow is — why should we believe that e.g.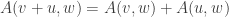 ?
?
…hmm, I guess the right-hand side corresponds to two stacked parallelograms, and the left-hand side corresponds to taking the common side and sliding it (leaving the other ends fixed) until you get one giant parallelogram. Sliding one side of a parallelogram along the line containing it doesn’t change its area, of course.
That’s exactly the right picture! If I could have drawn it in my comment I would have 😀
I will draw it in my next post! =)
I found that using polar coordinates (and a little trigonometry) gives a really nice proof. Let us rewrite the points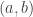 and
and 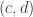 with polar coordinates:
with polar coordinates:


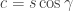

 and
and  , and the angle between them is given by
, and the angle between them is given by  . We can compute the area using the formula
. We can compute the area using the formula

We thus have the lengths of the parallelogram’s vertices
Using polar coordinates was nice in the fact that we did not have to express the lengths and the angle in the formula explicity in terms of ,
,  ,
,  and
and  , and it simplified very nicely instead.
, and it simplified very nicely instead.
Pingback: Happy tau day! | The Math Less Traveled