Differences of powers of consecutive integers

Patrick Vennebush of Math Jokes 4 Mathy Folks recently wrote about the following procedure that yields surprising results. Choose some positive integer $n$ . Now, starting with $n+1$ consecutive integers, raise each integer to the $n$ th power. Then take pairwise differences by subtracting the first number from the second, the second from the third, and so on, resulting in a list of only $n$ numbers. Do the same thing again, resulting in $n-1$ numbers, and repeat until you are left with a single number.

For example, suppose we choose $n=4$ , and start with the five consecutive integers $23, 24, 25, 26, 27$ . We raise them all to the fourth power, giving us

$279841,331776,390625,456976,531441$

Now we take pairwise differences: $331776 - 279841 = 51935$ , then $390625 - 331776 = 58849$ , and so on, and we get the new list

$51935,58849,66351,74465$

Repeating the difference procedure gives

$6914,7502,8114$

$588,612$

$24$

OK, so we get $24$ . So what?

Well, if you try enough examples, you may notice a surprising pattern. I’ll let you play with it for a while. Over the course of a few future posts I’ll explain the pattern and prove that it always holds—but the proof will be a really cool combinatorial one, with pretty pictures!

About Brent

Associate Professor of Computer Science at Hendrix College. Functional programmer, mathematician, teacher, pianist, follower of Jesus.

View all posts by Brent →

16 Responses to Differences of powers of consecutive integers

venneblock says:

January 29, 2012 at 10:47 pm

I can’t wait to see your proof. But mostly, I’m psyched to use $\LaTeX$ in this reply. I’m really rusty, though; let me test my powers of recall and try a joke:
$\frac{111111111}{9:53 p.m.}$
- Brent says:
  
  January 30, 2012 at 12:05 am
  
  To use $\LaTeX$ you have to write something like $ latex \sqrt{\pi}$ but without the space after the initial dollar sign, that is, just stick the word “latex” right after the opening dollar sign.
- Brent says:
  
  January 30, 2012 at 12:09 am
  
  Hmm, I don’t get it… but don’t tell me yet…
  - venneblock says:
    
    January 31, 2012 at 9:18 am
    
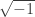    This sentence is a test for this whole $\LaTeX$ thing. $\sqrt{-1}$ like it!
    
    As for the joke, no spoiler yet — I’m hoping you find a solution to it that is as cool as the one you’ve promised for this problem!
  - venneblock says:
    
    February 27, 2012 at 10:27 pm
    
    Let me know when you need a hint. But I’ll probably hold off on relieving the suspense until you post the pretty pictures you promised.
Neural Outlet.. says:

January 30, 2012 at 1:30 am

A combinatorial proof with pretty pictures!? $Yay!$
Michael Paul Goldenberg says:

January 30, 2012 at 12:32 pm

Playing with Wolfram Alpha and using x^4 to start, I see that regardless of x, the first of the n + 1 consecutive integers (in this case with n = 4), the last pair will have a difference of 24, because the repeated pairwise subtractions will eliminate all the terms involving x and leave the difference of constants only. Hence, we can get the same result by taking the pairwise differences of n + 1 consecutive perfect nth powers. starting with 0^n and finishing with n^n.

Starting with n = 1, this gets very interesting indeed.
enderw88 says:

January 30, 2012 at 3:48 pm

I used a few LISP forms to calculate the first 15 values. The final number depends only on the exponent, not the seed integers picked. The value is “fibonacci” like in that if you start with 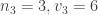$n_1=1, v_1=1$ , $n_2=2 v_2=2$ , $n_3=3, v_3=6$ … the $v_n=n_n v_{(n-1)}$

Here re the first 24 v’s:
((1) (2) (6) (24) (120) (720) (5040) (40320) (362880) (3628800) (39916800)
(479001600) (6227020800) (87178291200) (1307674368000) (20922789888000)
(355687428096000) (6402373705728000) (121645100408832000)
(2432902008176640000) (51090942171709440000) (1124000727777607680000)
(25852016738884976640000) (620448401733239439360000))
Michael Paul Goldenberg says:

January 30, 2012 at 4:15 pm

Funny how a flawed calculation can get you to do a lot of unnecessary work. At any rate, my initial hypothesis from your saying that you had a combinatorial proof coupled with 24 showing up in your example was correct: for a given power n and ANY n + 1 consecutive perfect nth powers starting with 0^n and finishing with n^n, following the rules will always reduce everything to n!

I’ll be interested in seeing the visual proof.
- venneblock says:
  
  January 31, 2012 at 9:24 am
  
  Michael, your “typo” (in quotes, because it’s not really an error) makes it look like you’re excited that the result is always n, when I know you mean n-factorial. This reminds me of the MathCounts coordinator who was moderating the Countdown Round and screamed, “What’s the value of FIVE?” The problem kids were supposed to solve was, “What is the value of 5!?”
  
  Like you, I’m very excited to see the visual proof!
Michael Paul Goldenberg says:

January 31, 2012 at 1:45 pm

@venneblock: I never get THAT excited about n.
- venneblock says:
  
  February 27, 2012 at 10:29 pm
  
  I do sometimes — but I usually have EEGIRT as the other six letters on my rack.
  - Michael Paul Goldenberg says:
    
    February 27, 2012 at 10:42 pm
    
    I never can figure out how to make and entire integer in Scrabble, can you?
Lev says:

February 2, 2012 at 6:51 pm

The pattern is the Pascal’s triangle with alternating algebraic sign in front of the coefficient. For $n=4$ you get: $(a+4)^{4}-4 \cdot (a+3)^4+6 \cdot (a+2) - 4 \cdot (a+1)^4 + a^4$ while $a$ is the starting integer. 🙂 Where do you get such cool brainteasers?
Pingback: Differences of powers of consecutive integers, part II | The Math Less Traveled
Pingback: Making our equation count | The Math Less Traveled