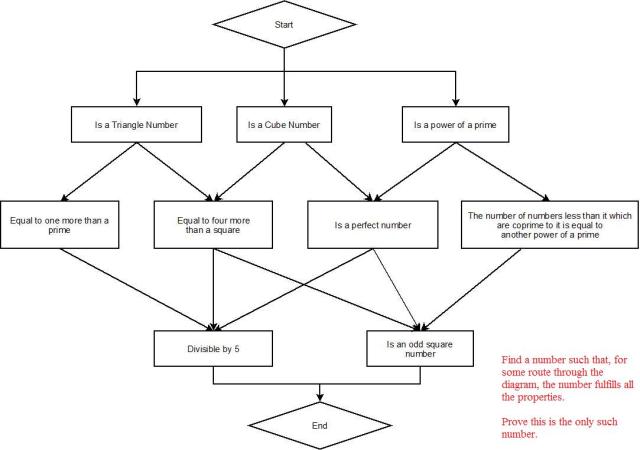
While poking around some old files I came across this puzzle:
(Click for a larger version.) I didn’t make it, and I have no idea where I got it from (do you know?). But in any case, wherever it comes from, I think it’s a really great puzzle. I did find the number that can make it through the diagram, but I never did completely finish proving that the solution is unique.
Can you solve it? Let’s see if we can prove it together. Please don’t post the number in the comments. But please do post proofs that certain combinations of nodes are impossible. For example, you might post a proof that no triangular number can be one more than a prime; that would mean the leftmost path is impossible.

I shall make a computer program that does this for me. Sometimes, computer programmers do not use brains, and instead uses brute force.
Let us know when your program finishes testing all nonnegative integers. We’ll wait.
(Hmmm.. I don’t think this is the intended solution, but goes down the right hand side of the diagram. Maybe they’re using a different definition of “number”, “coprime” or “another” to me.)
goes down the right hand side of the diagram. Maybe they’re using a different definition of “number”, “coprime” or “another” to me.)
I can prove that there’s no other solution going down the right hand side. Let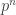 be a prime power with
be a prime power with 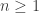 . Then a number less than
. Then a number less than 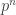 is coprime to
is coprime to 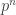 iff it doesn’t divide by
iff it doesn’t divide by  . Every
. Every  th number divides by
th number divides by  , so there are
, so there are 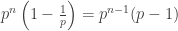 such numbers. This is clearly not a prime power unless
such numbers. This is clearly not a prime power unless 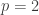 or
or 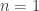 . In neither of these cases can
. In neither of these cases can 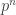 be an odd square.
be an odd square.
Hmm, good point, it’s a bit ambiguous. I think the intention is that there are zero numbers less than 1 which are coprime to 1, and 0 is not a prime power. I guess we should take “positive integer” as the definition of “number” for the purposes of this puzzle.
So far I got: No number can be 4 more than a square and also a odd square number. This is because there has to be two squares that differ by 4 which is impossible. The smallest square numbers are 0, 1, 4, 9, 16 and none of them differ by 4.
I can prove that we can’t go down the left hand side after. The triangle number divides by
divides by 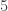 when
when  is of the form
is of the form 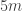 or
or  . Hence if our triangle number is one more than a prime then the prime is of the form
. Hence if our triangle number is one more than a prime then the prime is of the form 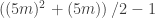 or
or  . These factor as
. These factor as  and
and  . These numbers have two factors each greater than
. These numbers have two factors each greater than  , so even when we divide by the
, so even when we divide by the  they wont be prime.
they wont be prime.
I have nearly solved the whole thing. All I have left to do is prove that (2,2) and (5,11) are the only positive solutions of the Mordell equation n^3=4+k^2 and prove that there are no odd cubic perfect numbers that are multiples of 5. My work can be found at https://drive.google.com/file/d/0B31DVyBvktcrc1dmNHZpTlZCLTA