Properties of orthogons I

First things first: from now on, when talking about polygons with only right angles, instead of calling them “orthogonal polygons” I’m going to start calling them “orthogons”, which sounds cool, is much less clunky than “orthogonal polygons”, and doesn’t seem to already be in use.¹ This name was recently suggested to me by Mark Dominus (who was the one who got me thinking about orthogons in the first place).

In my previous post, I posed several properties of orthogons and invited you to figure out why they are true. Here are my proofs.

Every orthogon has an even number of vertices.

Since every vertex is a right angle, the edges of an orthogon must alternate between horizontal and vertical. Hence there must be an even number of vertices; otherwise there would be two vertical edges or two horizontal edges meeting at a vertex, which does not make sense.
Orthogons only have two kinds of vertices: “right turns” and “left turns” (let’s suppose we always travel clockwise around the polygon).

Since writing this, I realized that it is probably easier to think of the vertices as either convex (the corner points towards the exterior of the polygon) or concave (the corner points towards the interior). I’ll use the letter X to stand for conveX vertices, and V for concaVe.

This way, we don’t have to worry about whether we traverse the polygon in clockwise or counterclockwise order (and besides, it can be confusing to figure out what “clockwise” vs “counterclockwise” even means when the polygon doubles back on itself a lot, as in the example shown below).

If you switch directions, left turns become right turns and vice versa. But describing vertices as convex or concave is independent of the polygon’s orientation. You can verify for yourself that the orthogon shown above has the vertex sequence $V^9 X^{13}$ , that is, nine concave vertices in a row followed by 13 convex vertices.

In any case, the reason there are only two types of vertices is simple: if you are travelling along an edge and come to a right-angle vertex, there are only two choices: turn 90 degrees to the left, or to the right.
Every (closed, non-self-intersecting) orthogon has four more right turns than left turns.

Again, the way I originally stated this, with left and right turns, is annoying: if you travel around an orthogon in the opposite direction, then it instead has four more left turns than right turns. We can state this in a much nicer way which is independent of direction: an orthgon always has four more convex vertices than concave.

Obviously this is true for a square, the one possible orthogon with four vertices: there are four convex vertices and no concave vertices. We can see that it also holds for the example orthogon shown above, with nine concave vertices and thirteen convex. Intuitively, the reason it is true in general is that every concave vertex is a turn in “the wrong direction” which needs to be “cancelled” by a convex vertex; on top of that, there need to be four convex vertices to make the whole thing “close up”.

Let’s see how to prove this more formally. We start from the fact that if you sum the internal angles of any polygon with $n$ vertices, you get $\pi(n-2)$ (that is, $n-2$ times $180$ degrees). When $n = 3$ this is just the familiar fact that the angles of a triangle sum to $\pi$ . But then for bigger $n$ , we can always cut up an $n$ -gon into $n-2$ triangles, and adding up the angles of all the triangles is the same as adding up all the internal angles of the whole polygon.

Now, suppose an orthogon has $x$ convex vertices and $v$ concave vertices, and hence $x + v$ vertices in total. Convex vertices have an internal angle of $\pi/2$ , and concave have an internal angle of $3\pi/2$ . Thus,

$\displaystyle x(\pi/2) + v(3\pi/2) = \pi(x+v-2)$

If we divide both sides by $\pi$ and multiply by $2$ , we get

$\displaystyle x + 3v = 2x+2v-4$

and then a bit of algebraic rearranging yields $x - v = 4$ .

Incidentally, this now gives us another way to see that there must be an even number of vertices: $x + v = x + (x - 4) = 2x - 4$ , which is clearly even.

The final property I stated—namely, that every viable sequence of V’s and X’s describes some orthogon—will have to wait for another post. I’ll give you a hint: the best way to prove this is to give an algorithm that takes a sequence of V’s and X’s as input and produces an actual drawing of an orthogon as output. (But for now it doesn’t matter if the drawing is horrible, just whether one exists!)

Wiktionary suggests that “orthogon” can refer to a right triangle or to a “rectangular figure” but I have never heard it used to refer to those things. Perhaps it is more common in other English-speaking countries?↩

About Brent

Associate Professor of Computer Science at Hendrix College. Functional programmer, mathematician, teacher, pianist, follower of Jesus.

View all posts by Brent →

10 Responses to Properties of orthogons I

Gesh says:

February 6, 2018 at 12:05 pm

The proof that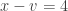 $x-v=4$ can be simplified by decomposing the orthogon as inductively built up by the attachment of a rectangle along an edge. Since the rectangle and the “smaller” orthogon both satisfy 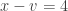$x-v=4$ (the former trivially, the latter by induction), it suffices to show that the number of vertices created/removed by the attachment satisfies $\Delta x-\Delta v=-4$ .

Now, note that at the interface of the attachment, we have four convex vertices bounding edges.
At each end, we have two possibilities: Either the vertices meet, in which case we lose two convex vertices, or they don’t, in which case the outer vertex remains convex and the inner vertex becomes concave. In either case, each end contributes $\Delta x-\Delta v=-2$ , for a total of $\Delta x-\Delta v=-4$ , which establishes the inductive step.
- Brent says:
  
  February 6, 2018 at 2:06 pm
  
  That’s a nice argument! I’m not convinced it’s that much simpler, though, since I think it still leaves something else to be proved: namely, how do we know that every orthogon can be built up inductively by gluing rectangles in this way?
  - Gesh says:
    
    February 7, 2018 at 10:57 am
    
    Point. One way to see this is by taking the partition of $\mathbb{R}^2$ induced by the edges of the orthogon, and dissecting the orthogon by that partition.
    
    Doing so reveals that I missed considering the case where the new rectangle gets attached to an L shape, but in that case the only complication is the loss of the concave vertex of the L shape and a convex vertex of the attached rectangle, for no net difference.
    (This has the technical complication of requiring the attachments to be ordered lexicographically in the grid, which can be avoided by proving the similar attachment lemma for C-shaped interfaces)
    
    Hopefully, this completes the proof – no bugs are visible to me ATM.
    - Brent says:
      
      February 7, 2018 at 5:53 pm
      
      Ah, nice! Yes, I think that works.
      - Gesh says:
        
        February 9, 2018 at 8:54 am
        
        Continuing upon the theme of evolving a rectangle into an orthogon, I have found a (not quite elegant) solution to your final question:
        
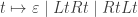        The viable sequences are those generated by rewriting $tRtRtRtRt$ subject to the rewriting rules $t\mapsto\varepsilon\mid LtRt\mid RtLt$ . In fact, since every viable sequence induces an orthogon isomorphic to the sequence rotated by any number of elements, we may WLOG consider the rewritings of $r=RtRtRtRt$ .
        
        In particular, any orthogon has a sequence of rewritings starting at $r$ and terminating in the sequence corresponding to the orthogon, with each step consisting of a single application of the rewrite rule. Let $x\mapsto\hat{x}$ be the map consisting of applying $t\mapsto\varepsilon$ everywhere, then constructing the orthogon corresponding to that sequence. Then $\hat{r}$ is a rectangle, and we are interested in completing $x\mapsto\hat{x}$ into a functor from sequences with rewriting to orthogons with evolution.
        
        Hence, all that needs to be done is to describe the evolution rules for inserting an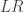 $LR$ or $RL$ pair at any point in a viable sequence. The evolution rules depend on the move prior to the inserted pair – I’ll describe the evolution rules $R\mapsto RRL$ and $R\mapsto RLR$ , with the $L$ case being isomorphic.
        
        So consider the a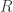 $R$ vertex, locally. To obtain a $RRL$ sequence, one attaches a rectangle to the outgoing edge of the vertex, continuing the incoming edge (and obtaining a shape like a cursive p).
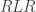        To obtain a $RLR$ sequence, one attaches a rectangle to the interior of the vertex’s corner (and obtains a shape like a W with orthogonal legs).
        
        Obviously, this construction has no local self-intersections. To avoid global self-intersections, make the attached rectangles decrease in size so as to never reach the other vertex on each edge.
        
        P.S. Sorry for the brevity, had to run. Hope the gist is clear.
        
        Brent says:
        
        February 10, 2018 at 5:27 pm
        
        Yes, this ends up being very similar to my proof. I’m going to make a new post with my proof shortly!
Gesh says:

February 6, 2018 at 12:06 pm

… For an appropriate value of “simplify”
Pingback: Properties of orthogons II | The Math Less Traveled
Pingback: Listing orthobraces | The Math Less Traveled
Pingback: Why drawing orthogons is hard | The Math Less Traveled