And now, the amazing conclusion to this series of posts on Neil Calkin and Herbert Wilf’s paper, Recounting the Rationals, and the answers to all the questions about the hyperbinary sequence. Hold on to your hats!

The Calkin-Wilf Tree

First, recall the Calkin-Wilf tree, defined as follows: the “root” of the tree is the fraction 1/1, and every node labeled in the tree has two “children”, with the left child labeled , and the right labeled . Here’s a picture of the first four levels of the tree (of course, the tree is infinite):

Now wait just one minute… those numbers look familiar! Let’s list those fractions in order, one level at a time, from left to right:

That’s right, it’s the hyperbinary sequence! In particular, the numerators are the hyperbinary sequence starting at index 0, and the denominators follow the same sequence, offset by one.

…but why?! The Calkin-Wilf tree is defined by a recursive rule for manipulating fractions, and the hyperbinary sequence is defined in terms of ways to write numbers as sums of powers of two… it certainly isn’t a priori obvious why these should have anything to do with each other!

Labelling the CW-tree

Let’s label the nodes in the Calkin-Wilf tree with positive integers, starting with 1 at the root and proceeding in order by levels, from left to right. This means that the fraction at node is —at least, that’s what we’re trying to prove! Here’s an illustration of our numbering scheme:

Now, what do you notice about the relationship between the label on a node and the labels on its children? It’s not too hard to guess the pattern: the left child of the node labelled is labelled , and the right child is labelled . How can we prove this?

Well, it’s certainly true for the root note: it’s labelled 1, and its children are labelled 2 and 3. Now we note that if the pattern holds for the node immediately preceding node —that is, the children of node are and —then the children of node come immediately after the children of , so they are numbered and . If you think about it, this is true regardless of whether and are on the same level, or is the end of one level and is the beginning of the next.

We can think of labelling each edge of the Calkin-Wilf tree with either a 0 or a 1: 0 for left edges, and 1 for right edges. Then taking all the zeros and ones along the path from the root to any node and sticking an extra 1 at the beginning gives us the label of that node in binary! For example, the path that goes left, left, right corresponds to 0, 0, 1, and adding an extra 1 to the front gives us 1001–which is indeed the binary representation of 9!

So, is it really true that the fraction at node is always ? It is indeed, and we now have the tools we need to see why. First of all, the root node of the tree—that is, node 1—is (by definition) , which is indeed . Next, suppose that the fraction at node is ; we need to show that the fraction at the left child (which is node ) is , and the fraction at the right child is . But this is now easy: by the way the Calkin-Wilf tree is defined, the left child is

The equality, of course, follows directly from the recurrence relation for the hyperbinary sequence! Likewise, the right child is

Solving the 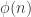mystery

As pointed out by JM, this connection with the Calkin-Wilf tree is exactly what we need to prove Fergal Daly’s conjecture about the number of primary occurrences of any given number.

We defined a primary occurrence simply as a number at an even position in the hyperbinary sequence. Of course, even-labelled nodes in the Calkin-Wilf tree are exactly the ones which are left children, and so the primary occurrences are the denominators of left children (equivalently, the numerators of right children). Also, since left children are always of the form , left children always have denominators bigger than their numerators. Finally, as you may recall, we showed earlier that every positive rational number occurs somewhere in the Calkin-Wilf tree, in lowest terms, exactly once.

Putting this all together: each primary occurrence of corresponds to a fraction in the Calkin-Wilf tree, where . And since every fraction occurs exactly once in lowest terms, there is exactly one such fraction for each positive integer which is relatively prime to . Of course, by definition, there are such numbers, so this is the proof of Fergal’s conjecture! There are exactly primary occurrences of , since that’s how many reduced fractions there are between 0 and 1 which have a denominator of .

Computing primary occurrences

The connection with the Calkin-Wilf tree also allows us to compute —that is, given any , we can efficiently (in time) compute all the primary occurrences such that !

How does this work? Well, if you remember, the Euclidan Algorithm gives us a way to find our way up the Calkin-Wilf tree from any starting fraction. Combining this with the relationship we discovered earlier between the label on a node and the labels on its children allows us to compute the label on the node where we started.

As an example, let’s compute one of the primary occurrences of 5. In particular, let’s do the one that corresponds to the fraction . Since 3 is smaller than 5, must be the left child of . 3 is bigger than 2, so is the right child of . Finally, is the left child of . Now we can work backwards: is node ; is to the left, so it’s node ; is to the right of that, so it’s node ; and is to the left again, so it’s node . Therefore is a primary occurrence of 5! We can also think of this more succinctly by recalling that paths in the Calkin-Wilf tree correspond to binary representations of the labels. So we can run the Euclidean Algorithm, getting a zero or one at each step, and then reverse them and put an extra 1 at the beginning to get the binary representation of the primary occurrence. To be more precise:

1. Start with the pair where is relatively prime to . Call the current pair of numbers .
2. Given , if then write . Otherwise write .
3. Repeat step 2 until reaching .
4. Read off the primary occurrence of by prefixing 1 to the reverse of the binary digits written over the arrows.

All of this leads to the following (somewhat mind-blowing) observation: the position of each primary occurrence of in the hyperbinary sequence is a proof (encoded in binary) that is relatively prime to the number that comes immediately before it.

To tie this all together, here’s a little Haskell program I wrote to compute primary occurrences:

import System.Environment (getArgs)
import Control.Monad (forM_)
import Data.Maybe (catMaybes)
import Data.List (sort)

-- Find a fraction in the Calkin-Wilf tree.  findCW a b computes the
-- location of a/b in the Calkin-Wilf tree, or returns Nothing if a
-- and b are not relatively prime.
findCW :: Integer -> Integer -> Maybe Integer
findCW 1 1 = Just 1
findCW a b | a < b  = left `fmap` findCW a (b-a)
           | a > b  = right `fmap` findCW (a-b) b
           | a == b = Nothing

left  x = 2*x
right x = 2*x + 1

-- Find the primary occurrences of n.
primaryOccs :: Integer -> [Integer]
primaryOccs n = sort . catMaybes $ [ findCW m n | m <- [1..n] ]

main :: IO ()
main = do (from:to:_) <- getArgs
          forM_ [read from..read to] $ \i -> do
            putStr $ show i ++ ": "
            putStrLn . unwords . map show . primaryOccs $ i

If there’s interest, I could write another post explaining how this program works in a bit more detail, but hopefully you can mostly understand what it’s doing from the preceding discussion. Let’s check that it works:

[brent@archimedes:~/teaching/mlt/hyperbin]$ ./prim-occs 2 16
2: 2
3: 4 6
4: 8 14
5: 10 12 16 30
6: 32 62
7: 18 22 24 28 64 126
8: 20 26 128 254
9: 34 46 48 60 256 510
10: 38 56 512 1022
11: 36 40 54 58 66 94 96 124 1024 2046
12: 44 50 2048 4094
13: 42 52 70 78 112 120 130 190 192 252 4096 8190
14: 68 80 110 122 8192 16382
15: 72 118 258 382 384 508 16384 32766
16: 92 98 134 158 224 248 32768 65534

Yup, looks good! And to show that it really is efficient, let’s use it to compute the primary occurrences of 1000 (yes, all 400 of them!):

[brent@archimedes:~/teaching/mlt/hyperbin]$ ./prim-occs 1000 1000
1000: 39770 42278 56024 58532 68396 70568 71444 75674 76688 85046 86480 92576 104030
... 386 more primary occurrences...
1071508607186267320948425049060001810561404811705533607443750388370351051124936
1224931983788156958581275946729175531468251871452856923140435984577574698574803
9345677748242309854210746050623711418779541821530464749835819412673987675591655
43946077062914571196477686542167660429831652624386837205668069374

On my computer this runs in about 0.03 seconds. Sweet! Note that the position of the final primary occurrence of 1000 has 303 digits–that’s approximately one centillion. I certainly wouldn’t want to go through the first one centillion numbers in the hyperbinary sequence looking for 1000 by hand, would you?

Further Reading

I hope you’ve enjoyed this little (1.5-year-long!) excursion into the fascinating world opened up by Calkin and Wilf’s paper. (I’ve sure enjoyed writing it!) If you’re interested in exploring more, I suggest looking at Roland Backhouse and João Ferreira’s paper, Recounting the Rationals, Twice! which also explains the connection to another famous tree of fractions, the Stern-Brocot tree. If you’re interested in the computational aspect of the hyperbinary numbers, have a look at Enumerating the Rationals, by Jeremy Gibbons, David Lester, and Richard Bird.