You have a function and want to prove it is a bijection. What can you do?
By the book
A bijection is defined as a function which is both one-to-one and onto. So prove that is one-to-one, and prove that it is onto.
This is straightforward, and it’s what I would expect the students in my Discrete Math class to do, but in my experience it’s actually not used all that much. One of the following methods usually ends up being easier in practice.
By size
If and
are finite and have the same size, it’s enough to prove either that
is one-to-one, or that
is onto. A one-to-one function between two finite sets of the same size must also be onto, and vice versa. (Of course, if
and
don’t have the same size, then there can’t possibly be a bijection between them in the first place.)
Intuitively, this makes sense: on the one hand, in order for to be onto, it “can’t afford” to send multiple elements of
to the same element of
, because then it won’t have enough to cover every element of
. So it must be one-to-one. Likewise, in order to be one-to-one, it can’t afford to miss any elements of
, because then the elements of
have to “squeeze” into fewer elements of
, and some of them are bound to end up mapping to the same element of
. So it must be onto.
However, this is actually kind of tricky to formally prove! Note that the definition of “ and
have the same size” is that there exists some bijection
. A proof has to start with a one-to-one (or onto) function
, and some completely unrelated bijection
, and somehow prove that
is onto (or one-to-one). Also, a valid proof must somehow account for the fact that this becomes false when
and
are infinite: a one-to-one function between two infinite sets of the same size need not be onto, or vice versa; we saw several examples in my previous post, such as
defined by
. Although tricky to come up with, the proof is cute and not too hard to understand once you see it; I think I may write about it in another post!
Note that we can even relax the condition on sizes a bit further: for example, it’s enough to prove that is one-to-one, and the finite size of
is greater than or equal to the finite size of
. The point is that
being a one-to-one function implies that the size of
is less than or equal to the size of
, so in fact they have equal sizes.
By inverse
One can also prove that is a bijection by showing that it has an inverse: a function
such that
and
for all
and
. As we saw in my last post, these facts imply that
is one-to-one and onto, and hence a bijection. And it really is necessary to prove both
and
: if only one of these hold then
is called a left or right inverse, respectively (more generally, a one-sided inverse), but
needs to have a full-fledged two-sided inverse in order to be a bijection.
…unless and
are of the same finite size! In that case, it’s enough to show the existence of a one-sided inverse—say, a function
such that
. Then
is (say) a one-to-one function between finite equal-sized sets, hence it is also onto (and hence
is actually a two-sided inverse).
We must be careful, however: sometimes the reason for constructing a bijection in the first place is in order to show that and
have the same size! This kind of thing is common in combinatorics. In that case one really must show a two-sided inverse, even when
and
are finite; otherwise you end up assuming what you are trying to prove.
By mutual injection?
I’ll leave you with one more to ponder. Suppose is one-to-one, and there is another function
which is also one-to-one. We don’t assume anything in particular about the relationship between
and
. Are
and
necessarily bijections?

Cheeky example: S: Nat -> Nat is injective so take f = g = S!
By S do you mean the successor function? That’s a good example, not cheeky at all!
Pingback: Not injective, not surjective, but bijective – The nth Root
I did mean successor, yes!
If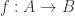 is one-to-one, then
is one-to-one, then  . Similarly, if
. Similarly, if 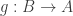 , then
, then  . If both are true, then
. If both are true, then  and a bijection exists between
and a bijection exists between 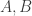 , but there’s no guarantee that either
, but there’s no guarantee that either 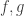 are bijections.
are bijections.
If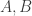 are finite, then (as you argued in “By Size”), both
are finite, then (as you argued in “By Size”), both 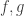 are bijections. But if they are infinite, then there are
are bijections. But if they are infinite, then there are  that are one-to-one, but not onto. Proof: Since
that are one-to-one, but not onto. Proof: Since  is infinite, there exists a
is infinite, there exists a  that is one-to-one but not onto, so if
that is one-to-one but not onto, so if  is one-to-one, then
is one-to-one, then  is one-to-one, but not onto.
is one-to-one, but not onto.
This is one of my favorite ways to show . It usually isn’t hard to come up with the necessary injections, even if it is hard to find a bijection. It is easy to show that
. It usually isn’t hard to come up with the necessary injections, even if it is hard to find a bijection. It is easy to show that 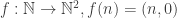 and
and  are both one-to-one, It is harder to come up with an easy-to-describe bijection.
are both one-to-one, It is harder to come up with an easy-to-describe bijection.
Indeed! I think I will probably write about this in an upcoming post. One fun thing is that the proof of the Schröder-Bernstein theorem is actually constructive, so in theory you can take any two injections and actually use them to construct a bijection. But indeed, there is no guarantee that the resulting bijection is easy to describe. I am still trying to work out how to describe the one generated by your pair of injections between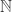 and
and 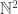 . It’s something like this: any number can be written in the form 2^2^…^m where
. It’s something like this: any number can be written in the form 2^2^…^m where  is not a power of two, that is, a tower of zero or more 2’s with a final power of
is not a power of two, that is, a tower of zero or more 2’s with a final power of  on top. (If
on top. (If  is not a power of two then
is not a power of two then 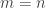 .) If
.) If 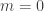 or
or  has prime factors other than 2 or 3, then send
has prime factors other than 2 or 3, then send  to
to  . Otherwise, if
. Otherwise, if  is a power of two, send it to
is a power of two, send it to 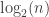 ; finally, if
; finally, if  , send it to
, send it to 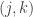 . It’s very non-obvious that this is a bijection (and I might have even gotten the description wrong)!
. It’s very non-obvious that this is a bijection (and I might have even gotten the description wrong)!
Pingback: Competitive programming in Haskell: permutations | blog :: Brent -> [String]